Cálculo del tren epicicloidal
El cálculo de la relación de multiplicación o desmultiplicación de un tren epicicloidal puede parecer algo ... retorcido 
. Aquí hay una página de cálculo para facilitarle la tarea.
Un tren de engranajes epicicloidal es un sistema de engranajes particular que consiste en una corona, un portasatélites que soporta varios satélites y un planeta.
Cálculo del tren epicicloidal (simple)
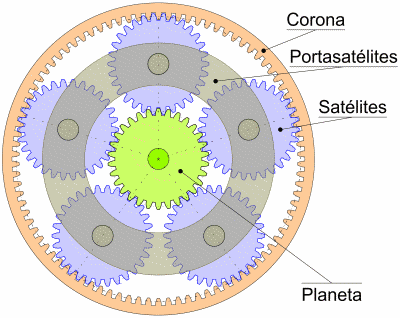Tren epicicloidal
Relación de multiplicación entre el portasatélites y el planeta: 4,00
Por 1 revolucione del portasatélites, el planeta es 4,00 Revoluciones
Diámetros primitivos |
|---|
| Corona: |
120,00 mm |
| Satélites: |
40,00 mm |
| Planeta: |
40,00 mm |
Satélites |
|---|
| Número de dientes de los satélites: |
20 |
| Número óptimo de satélites: |
5 |
Velocidades angulares |
|---|
| Corona: |
0,00 rd/s |
| Portasatélites: |
50,00 rd/s |
| Planeta: |
200,00 rd/s |
Par resultante |
|---|
| El par resultante en el planeta es de |
2,50 N.m |
Terminología del tren epicicloidal
Corona
Es un anillo dentado que tiene la particularidad de que la parte superior de los dientes está orientada hacia adentro.
Portasatélites
Es una meseta alrededor de cuyos ejes giran los satélites. Puede ser fijo o móvil. Si es fijo, entonces el sistema se comporta como un inversor de la dirección de rotación, y la relación de multiplicación o de sobremarcha es simplemente una función de la relación entre el número de dientes de la corona y el número de dientes del planeta, al menos en el caso de un simple tren epicicloidal.
Satélites
Estos son los engranajes montados en el portasatélites que mueven (o son movidos por) este último cuando gira. Cuando el portasatélites está fijo, los engranajes solo giran sobre sí mismos.
Planeta
Este es el planeta colocado en el corazón del sistema.
Diámetro primitivo
El diámetro primitivo se mide en el promedio de los puntos de contacto de los dientes de dos elementos de engranaje.
Módulo
El módulo no es específico de los trenes de engranajes epicicloidales, sino de los engranajes en general. Corresponde a la dimensión estandarizada de un diente de engranaje. Un módulo "1" da una distancia de 3,14 milímetros entre 2 dientes. Un módulo "2" dará así una distancia de 6.28 milímetros. Esta distancia se mide en el diámetro primitivo, siguiendo la curva.
Al conocer el módulo y el número de dientes, obtenemos directamente el diámetro primitivo mediante una simple multiplicación. Por ejemplo: un engranaje con 20 dientes de módulo "2" tendrá un diámetro primitivo de 40 mm.
El módulo suele ser un número entero o, en ocasiones, un submúltiplo simple (p. ej.: 1.5). No tiene una unidad.
Algunos módulos estándar son: 1 - 1,5 - 2 - 2,5 - 3 - 4 - 5 - 6
Ventajas del tren epicicloidal
Los engranajes planetarios proporcionan algunas ventajas interesantes, tales como:
- Menos espacio y peso en potencia y par equivalente.
- Pares transmisibles más altos.
- Mejor distribución de fuerzas en los engranajes, lo que reduce considerablemente las fuerzas soportadas por los rodamientos.
- Mejor rendimiento, o más bien, menores pérdidas (si son de buena calidad).
- Árboles de entrada y salida colocados en el mismo eje.
Desventajas del tren epicicloidal
Desafortunadamente este tipo de engranaje también tiene algunas desventajas:
- Mayor costo de fabricación.
- Hiperestatismo, que exige una calidad de fabricación impecable.
Número máximo de satélites
Dependiendo de la configuración, es posible colocar más o menos satélites en el portasatélites. A mayor número de satélites, mayor podrá ser el par transmisible. Sin embargo, hay un límite máximo que no puede ser excedido. Lo encontrará en los resultados.
Calcular la velocidad de salida de un tren epicicloidal
La velocidad de rotación de salida de tal sistema de engranajes es una función del elemento impulsor, la parte fija y el elemento de salida. Introduzca la velocidad de rotación inicial y elija el elemento al que se aplica. Los resultados mostrarán las velocidades angulares de cada elemento.
Calcular los pares transmitidos por los trenes epicicloidales
El par transmitido es inversamente proporcional a la velocidad de rotación de los dos elementos móviles.
Al introducir un par de entrada en el elemento impulsor, obtendrás el par de salida recibido en el elemento accionado.
Para obtener más información sobre el par y la potencia de un mecanismo giratorio y cómo calcularlos, visite la página "Cálculo de par y potencia".
Condición del número de dientes
Es necesario respetar la condición del número de dientes para que se pueda realizar el montaje mecánico. Después de deducir el número de dientes de los satélites, el motor de cálculo de esta página comprueba que se respeta esta condición. Si recibe un mensaje de "error" que te indica que esta condición no se respeta, generalmente es suficiente con aumentar o disminuir un diente de los dos planetarios. Puede realizar varias pruebas según sea necesario.
Condición para respetar: el anillo debe tener tantos dientes como el número de dientes del planeta agregado a los de dos satélites.
Además, será necesario adaptar el número de satélites para obtener un sistema equilibrado, respetando otra condición: el número de dientes del planeta sumado al número de dientes de un satélite, todos divididos por el número de satélites debe dar como resultado un número entero.
Esta última condición también se verifica en el motor de cálculo, lo que hace posible visualizar el número óptimo de satélites en los resultados.
En algunos casos, el resultado de la cantidad de dientes de los satélites puede ser muy bajo, o incluso demasiado bajo. El límite mínimo teórico se establece en 3 dientes por satélite. Para ser realista, será prudente revisar los datos iniciales para que este número de dientes sea mayor. Si es posible, mayor de 10.
Lista de páginas de cálculo